Notes

Bongard Solvers

2020-05-10

About

Bongard problems (BPs) are little puzzles of logic, meaning, and pattern recognition, in which the task is to figure out how to draw a categorical boundary between two sets of simple images.

Despite their elementary appearance, Bongard problems require the solver to work at multiple levels of abstraction and organisation, and to perceive sometimes subtle properties and relations from the right point of view. Thanks to their compactness and highly general nature, the puzzles remain a challenge even for contemporary computer vision based solver systems.

This piece is a look at some approaches that have been explored in automated Bongard problem solvers as well as some thoughts on what mechanisms could be further explored in this domain.

Introduction

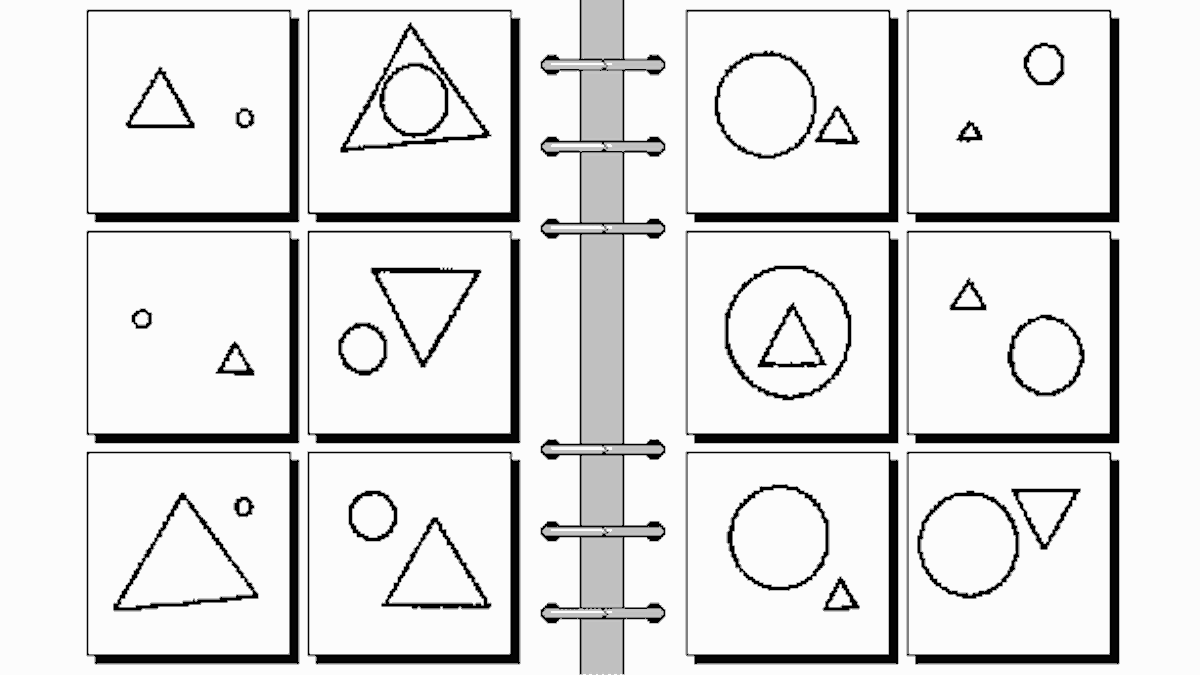
In the standard Bongard problem there are two sets of images, one on the left and one on the right. The images on the left side share some common property that none of the images on the right have, and vice versa. The challenge is to find and articulate these image set descriptions by which the two sets can be cleanly divided. See the image below for an example.

Bongard problems are named after Russian computer scientist Mikhail Bongard who studied pattern recognition in the 1960s and presented a collection 100 problems of this kind in his book Pattern Recognition (1967). BPs were introduced to a wider audience in the AI prospects chapter of Douglas Hofstadter's book Gödel, Escher, Bach (1979). I recommend Hofstadter's inspired introduction to the puzzle. Hofstadter's PhD student Harry Foundalis gives a long form treatment of BPs in his thesis (2006).

While some progress has been made in solving BPs using all kinds of clever programs, the puzzles remain challenging to solve for both humans and machines alike. Despite the advent of deep learning and mature neural network based image processing systems, there is still much to study in this microdomain. The diversity and subtlety of the more involved puzzle instances suggests that general BP solving could well be human-hard.

In any case Bongard problems lead the curious solver — the solver designer — to the hardest questions in general machine learning: What are the right representations? How does meaning enter a problem domain? What determines the salience of each available piece of information? How does the "big picture" emerge from minute details?

In other words, Bongard problems continue to provide a highly accessible path to some of the deepest questions in all of computing.

See Harry Foundalis' index of Bongard problems for many more instances of Bongard problems.

Example Bongard problem
Image: An example of a Bongard problem. The six images on the left each share a common natural language description, in this case something like 'the circle is smaller than the triangle'. Similarly all the images on the right conform to the rule 'the triangle is smaller than the circle'. In Bongard problems the task is to find and articulate these image group descriptions that define the categories on each side. In some cases the right hand side is a true opposite or negation of the rule on for left side, but this is not generally the case. The skeuomorphic framing in the picture plays no role in the puzzle.

Hofstadter and GEB (1979)

In GEB, Hofstadter describes Bongard problems as challenges for pattern recognisers, whether human or machine or otherwise. In his view, BPs are far from being simple toy puzzles: the mechanisms embedded in these problems go right to the core of cognition.

"Skill of solving Bongard problems lies very close to the core of 'pure' intelligence, if there is such a thing. Therefore it is a good place to begin if one wants to investigate the ability to discover 'intrinsic meaning' in patterns or messages."

Refining in stages

Hofstadter gives a class based description for the problems: the boxes on the left form Class I and boxes on the right form Class II. The task is to find and articulate the difference between the two classes. To help analysis and discussion, the images can be labelled like so:

          I-A  I-B	 II-A II-B
          I-C  I-D	 II-C II-D
          I-E  I-F	 II-E II-F

Hofstadter proposes a staged approach to programmatic BP solving. The early stages are more fixed and standardised, while higher stages are more flexible and expressive. The early pre-processing stages build a vocabulary of salient features (line segment, curve, vertical, black, small, pointy, ...). Later steps build shapes: triangles, circles, vertices, cusps, and more. These building blocks are then used in later stages to find the answer.

To Hofstadter, the interesting part in the solving process happens in the transition point, where a human solver moves from unconscious pattern recognition to deliberate, conscious cognition. All through the stages, the situational "picture" is always tentative in the solver's mind, instantaneously reconstructed from lower stage details. Higher level descriptions emerge from lower level details through a process of description refinement.

An example of refinement could go something like:

  1. three shapes
  2. three white shapes
  3. two triangles and a circle
  4. one large shape and two small shapes
  5. a circle with the same kind of shape on the inside and outside

The challenge in refinement is that language is fuzzy and pliable. An "almost-circle" is a valid visual construct and concept. At the same time our descriptions can get overloaded, become too precise, and lose track of the puzzle instance. Correct solving is about recognising the right answer, the classifier rule, at the semantic level appropriate to the puzzle.

Hofstadter gives a general BP solving algorithm:

  1. make tentative descriptions for each box
  2. compare descriptions across all boxes
  3. restructure descriptors by adding and discarding information, or by "viewing things from a different angle"
  4. iterate from 1. until a true classifier is found.

Solver concepts

In GEB, Hofstadter outlines an agent based Bongard problem solver and various components and concepts that would feature in such a system. Variations of these components find their way in many of the systems developed by the Fluid Analogies Research Group, FARG, that Hofstadter later founded at Indiana University.

To Hofstadter, one clue about higher level descriptions that frequently capture the solution lies with high variety and high diversity. The trick is to pool all individual descriptions and see where and how similarities and differences form.

Towards the end of the BP segment in GEB, Hofstadter proposes a nice analogy for puzzle solving. Solving BPs can be viewed as a kind of a science, where the task is to discern patterns in the Bongard problem world, and through experimentation and theories find the "laws" that accurately describe what's going on. Hofstadter stresses that this is not a world of Kuhnian paradigm shifts, but a different kind of science, where discoveries occur simultaneously at all levels of complexity. The fluidity of descriptions, the solution fragments, means that shifts happen all over. At best, some "revolutionary" discoveries occasionally have wider effects in the world.

In essence, Hofstadter argues that the evolutionary mechanism of description generation stays the same all the way up and down the levels of detail and complexity. The same mechanism is in charge of early and later stage pattern recognition. Indeed, this could be the case for all cognition.

"It is doubtful that in humans the sub-network of concepts relevant to these puzzles can be easily separated out from the whole network. Rather it is much more likely that one's intuitions gained from seeing and handling real objects [..] play an invisible but significant guiding role in the solution of these puzzles."


Phaeaco (2006)

Summary

Phaeaco is a "cognitive architecture for visual pattern recognition" as well as a Bongard solver implementation. Phaeaco was developed by Harry Foundalis between 1995 and 2005 and is comprehensively present in his PhD thesis (2006) that he completed under the supervision of Douglas Hofstadter at Indiana University.

Phaeaco is very much a "Hofstadterian" architecture: the BP solver implements many of the ideas Hofstadter was thinking about in GEB. Phaeaco is one several systems designed by Hofstadter's group for studying cognitive behaviour — solving as many BPs as possible was not a primary goal with Phaeaco.

At the heart of the system is a "psychologically plausible" difference metric by which images and image sets are compared. Phaeaco follows an evolutionary process of sorts, where various operators process and transform representations derived from image data. Together, the operator actions result in a pool of structures and partial descriptions for the images in the target instance. These descriptions and candidate solutions are then compared and evaluated. If a sufficiently discriminative property is found by the high level solution operators, a final natural language description is produced, and the instance is solved.

In other words, Phaeaco is a complete multi-modal solver system. Phaeaco can process raster image data, pixel input, and process that into abstract representations using a family of feature detectors and extractors. These operators carry and apply the labelling provided by the detector author. At a higher, more "analytical" level, Phaeaco works with figure group statistics and makes use of learned, persisted concepts stored in long-term memory.

Phaeaco is able to solve a range of BP problems, at least a dozen or so of the original 100. Foundalis emphasises that the architecture could be extended further, but the system has not been developed since. Phaeaco fares "nearly as well as humans" on the puzzles it manages to solve.

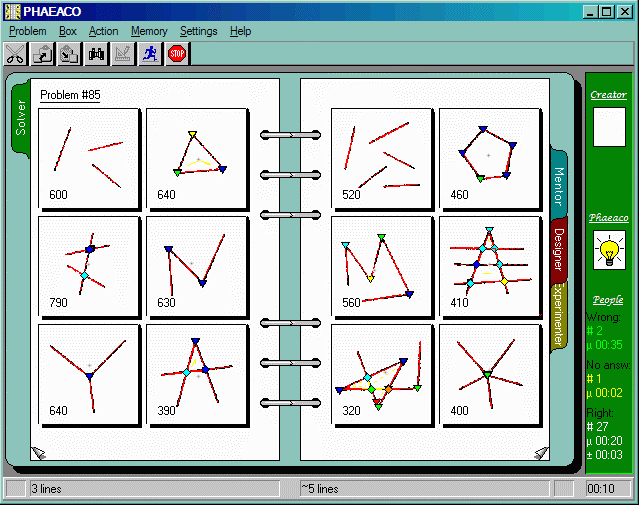
Notably, Phaeaco also features a complete graphical user interface with which users can operate the solver. There's a mentor mode in which users can give new labels to visual constructs. The larger Phaeaco system also features an authoring program that allows users to conveniently create new instances of Bongard problems.

Bongard's world

In his thesis, Foundalis points out that Bongard's original interest was specifically in the automation of visual perception. The puzzles are designed to put a pattern recognition system to the test. Due to the limited computing capabilities of the day, Bongard focused his effort on the limited domain of "simple" geometric images. Fortunately, it turned out that these domains proved perfectly adequate for studying both pattern recognition as well as the supposedly cognitive mechanisms that enable humans to solve these problems.

Foundalis defines the BP solving task as the discovery of a statement that describes image boxes on the left side of the problem, but none of the boxes on the right. In a sense the emphasis is on the the natural language output as learned from input images.

Foundalis makes some general observations about the properties of the domain:

Foundalis uses the term "visual pattern" to describe the kinds of abstract or generalised properties that are extracted from concrete visual stimuli in the images. This notion leads to a "statistical average" of said properties, and aggregate values that balance multiple perceived features. In other words Foundalis sets up a quantitative metric for features extracted from images.

There are a some meta level considerations for BP solving as well. Bongard uses the notion of priming in his original problem set, where ideas or patterns are introduced first in a straightforward setting, only to be reused and remixed in subsequent problems.

Humans and pattern matching

When computers, and the software systems running on them, are not capable of solving a problem by themselves, humans have to lend a helping hand. This leads to questions about the degree to which humans can and are allowed to assist a solver system in its task. In the context of BPs, it's not clear how much human assistance is reasonable, and how one can even measure the degree of automation.

In the early days of AI, it was common for the "burden" of the real world to be stripped away, leaving only the "purified problem" behind to be tackled. In this way any "solving" is typically so "crystallised", so removed from reality, that the solutions and approaches do not scale at all to new circumstances. This research led to the expert systems industry, which burned brightly in the 70s and enjoyed some commercial success, but hardly advanced the field.

Foundalis points at system RF4 (1996) as an example of this kind over-simplification. RF4 searches a space of formulas of first-order logic, the formulas in this context being abstract representations of Bongard Problems. The trick is that the formulas are human generated, and so the system is already leveraging human pattern matching ability under its own operation. Foundalis concludes that logical formulas, with a human mediator, are the "wrong medium" for representing BP input, because either:

  1. The logical description is "honest", but too long and unwieldy for manipulation, or
  2. The description is short, but "dishonest", giving away predicates crucial for the solution.

Hofstadter and his group have been vocal opponents of this line of thinking for a long time (see, e.g., Chalmers 1992, included in Hofstadter 1995). For a further critique of RF4 and an overall look at ways of thinking about Bongard problems, see Alex Linhares' somewhat more philosophical study of Bongard problems (2000).

A more transparent way for humans to assist solvers is through mentoring. In his thesis Foundalis presents the work of one of Bongard's own students, V. V. Maksimov, who decided to explicitly recruit the human to assist with pattern detection work. Maksimov's approach (1975) revolves around "training sets" with which a human user can, through feedback, incrementally teach concepts to a recogniser program. Working with highly constrained computing resources, Maksimov's program was able to solve simplified variations of Bongard problems by way of a combinatorial search.

Foundalis doesn't really emphasise the role that he himself played in constructing the detectors that power Phaeaco, but the reality is that at some point some human contribution is needed because of the grounding problem of language. No solver system can generate natural language solutions without being told what names to use for visual patterns and concepts.

At another level, it is reasonable to consider what kinds of designs are reasonable in Bongard problems. Should BPs be limited to geometry alone and is that even possible? Is 3D perception okay? Is pixelated perception, limitations on visual fidelity, part of the problem? Is grounding BPs to human perception reasonable? How about world-understanding, the human experience of motion, navigation, gravity, culture, meta-levels of meaning, etc.? Certainly there are many ways to simplify the general BP domain.

In Foundalis' view, distinction between "ill-defined" and "valid" BPs is arbitrary and self-serving, interfering with the flexibility of concepts and the "real" processes of cognition that he is interested in. On the other hand Foundalis has himself proposed some general rules for Bongard problems.

Finally, Foundalis also makes the case that BPs are (supposed to be) universal and objective, referencing various anthropological touchstones of figure and shape. Indeed one can argue that creativity is the only limitation when it comes to BP design. And in that case the challenge of Bongard problem synthesis is a rather interesting one.

Phaeaco

Phaeaco the app presents the user with a graphical interface for working with Bongard problems. Through this interface, the user can view the internal state of the solver, how Phaeaco is viewing the problem, at any point in time.

Phaeaco
Image: A screenshot of Phaeaco in action, from Foundalis (2006). Notice the markers indicating detected features, overlaid on top of the problem instance. The detected descriptions are given at the bottom of the screen: '3 lines' on the left, '~5 lines' on the right.

According to Foundalis, the Phaeaco solver operates in three stages: the hardwired, the holistic, and the analytic stage. The hardwired stage is in charge of trivial visual perception, such as existence. In the holistic stage, features are generated and processed and studied in aggregate, in search of clear global properties. In the final analytic stage, Phaeaco looks at the images in more detail, and tries to extract more descriptions for each of them. All the while, comparison operators are working on the generated structures, looking for similarities.

Foundalis offers another way to look at pattern detection in Phaeaco, by dividing the operators in two groups: the "retinal" and the "cognitive". Building up from the initial input set of 12 boxed images presorted in two groups, Phaeaco does various types of input processing and then works with generated representations. Foundalis argues that the focus is on the "cognitive" mechanisms much more than on the "retinal" image processing. In working with the same structures, both kinds of operators are still in close interaction and continually influence one another. This is very much the blueprint for general Hofstadterian "codelet architectures" as explored in Copycat and other FARG projects (Hofstadter 1995).

Some purpose-built operations and abilities that Phaeaco can make use of:

As a general design principle, Foundalis offers that building mechanisms for solving hard BP instances typically renders easier problems solved as well. Meeting the needs of the difficult customer makes your product better overall. One can even view BP solver design as a challenge where the task is to develop sufficiently abstract and general mechanisms — as well as sufficient image processing — such that human-hard BP instances become solvable, and therefore all of the easier ones as well.

Foundations

One of the central pieces of all machine learning and perhaps even AI is knowledge representation. In his thesis, Foundalis gives what can be described as "the FARG view of concept representation". In his words, Phaeaco merges the exemplar and prototype concept theories. These are best understood in historical context.

Plato was interested in abstract and pure ideas, "the Theory of Forms", and was keen on arguing by and about definitions. Aristotle's thinking revolved around the notion of essence and elementary categories, conceptual primitives, such as substance, quantity, relation, position, action and passion. The genus and the differentia, general category membership and distinguishing features.

This classical theory was criticised for failing to account for fuzzy category membership, the experience of distributions along a spectrum. There are degrees of membership, membership is drawn from continuous attributes. The world can be viewed through a statistical lens.

One remedy for the classical system came in the form of what can be described as a procedural approach: categories have a central core, but also an identification procedure that defines some characteristic features of the category. Proponents of prototype theory believe that the core of categories is captured by summary representations, or "best examples", representative sets of features weighted by frequency relative to the population. This somewhat mechanical category definition scheme still has no story for continuous attributes, or thresholds. Schemata theory aims to address some of these concerns.

Exemplar theory argues against summary representations, suggesting that a category is little more than a collection of examples. There is no definition, only comparisons. This results in easy typicality and borderlines case resolution. Example set and comparisons also give rise to natural intransitivity, in that any given specimen can be a member of two categories, without requiring that both categories collapse into one. Foundalis gives a great example: a car seat is a kind of a chair, and chairs are one type of furniture, but car seats are not (generally!) furniture. Still, exemplar theory has some weaknesses, particularly in category assignment and similarity measures as well as in how examples get stored.

Phaeaco uses internally a representational structure based on the generalised context model, GCM. In this model the similarity of two objects, two exemplars, is a function of the weighted Manhattan distance between them in feature space. The weight vectors of this feature space are context dependent. In standard GCM, category membership is measured as similarity within a given category over the sum of all similarity across all categories. Phaeaco uses a more elaborate statistical computation for determining membership.

Phaeaco attempts to combine some aspects of prototypes, exemplars and GCM all in one. It starts off more prototype oriented, but then turns more and more statistical as the operator actions begin to pile up.

FARG concept architecture

Before diving into the details of the Phaeaco implementation, Foundalis gives a short introduction to "Hofstadterian" systems and the general concept architecture developed at FARG. The Copycat system (later Metacat, see Hofstadter 1995), "analogies in the letter-string domain", is perhaps the truest implementation of the architecture.

At the centre of the FARG model lie concept cores, ideal concepts in the Platonic sense. There is a concept network, a graph or network of directed links, forks, bi-directional links, self-reference and higher order structure. A key property of this setup is the "conceptual slippage" between concepts sufficiently close by in the network. This makes concepts and the relations between them fluid.

The nodes in the concept network, also known as Slipnet in some systems, have a continuous quantity known as activation that drives the dynamics in the network. Action begins at the conceptual core, and spreads to neighbouring nodes around the core, the halo. Each link in the net has a label, and is fully addressable. Node activations act on the links, bring concepts closer to one another by shortening links, "shrinking the cable". This effect fades over time.

Another key structure in the architecture is the workspace, the short-term memory. The workspace is where the operators perform their actions, typically constructing and disassembling knowledge representations. In the workspace larger structures are built from simpler ones, and old structures are re-purposed. The work taking place in the workspace is influenced by global and structure-local properties such as importance (a function of activation) and structural unhappiness (the "level of integration" relative to the reset of the workspace). The salience of any given representation is a higher order function of both importance and unhappiness. Temperature, not in use in Phaeaco, is a global measure of disorder, and can be viewed as how much the overall system "likes" a particular answer.

Finally, there's the codelets and the coderack, the operators and their warehouse. These are the functional labourers that make things happen in the workspace. The codelets have no pre-designed plan, there's only a global emergent one. Codelets are simple procedural blocks that define an operation. The coderack is a structure for accessing and selecting codelets for execution. The urgency of a given codelet is the probability of it being selected off the coderack.

The codelets can be divided into two groups: bottom-up codelets, which work on structures in the workspace without direction, and top-down codelets, which work on the workspace with an eye towards higher level structures. In Phaeaco, these two perhaps map to the "retinal" and the "cognitive" modes of operation.

Representations in Phaeaco

Phaeaco relies on developer defined conceptual primitives for its knowledge representations. The primitives include things such as "point" and "line segment", etc. Additionally there are user provided concepts, labels for things generated from these primitives, such as "triangle". Phaeaco generates working representations on the fly from "retinal level" image processing inputs, building things up from the lower level inputs using codelet operators.

The representations in Phaeaco are stored in a concept net where nodes are linked to one another in a "nearly hierarchical manner" by level of detail. Representational characteristics, such activation and numerosity are carried along in the nodes of the network.

In Phaeaco the codelet library, which effectively captures both the concept generation and grounding in the form of labelling, is extensible, even at runtime. In other words, what Phaeaco can "see" is not predetermined, but rather the result of the interactions in the workspace and the dynamic concept net. The overall process is probabilistic. Activation, modelled as a sigmoid function, influences the workspace. Threshold boundaries keep things within human perceptual range .

Some of the representations in Phaeaco, all coded up in the detector operators:

Here again, the role of the human designer is evident. What is a reasonable domain for primitives, how large is a reasonable library of visual primitives?

It's clear that the Phaeaco architecture requires at least some and possibly quite a bit of human effort for each perceptual primitive — and the notion of primitive is quite slippery in the BP context. General visual cognition is hard.

Foundalis gives a list of things that Phaeaco cannot do (but, he claims, could be made to do):

Visual pattern matching

For Hofstadterians, analogy is the core of cognition, and pattern matching is the core of analogy-making:

"Process of inexact matching between prior categories and new things being perceived is analogy-making." (Hofstadter)

Pattern matching is the art of seeing similarity in things. In Phaeaco, the task is to establish the perceptual difference and therefore similarity between items for the purpose of grouping and categorisation.

The Phaeaco visual pattern matching algorithm runs roughly as follows:

  1. Find matching feature nodes
  2. Find matching numerosity nodes
  3. Calculate weighted feature difference
  4. Find matching structures
  5. Use structural difference to compute similarity
  6. Group formations based on exemplars
  7. Update patterns

In Phaeaco, a rather involved independent process turn visual patterns into concepts:

  1. Maintain a persisted memory of patterns
  2. If a new pattern is found to match an existing concept well enough, update the concept with the new pattern. Otherwise, form a new one concept from the pattern.
  3. When category membership changes, update all related feature node statistics
  4. Evolve the concept net with activations (thus enabling learning)
  5. Update links as associations and relations, using variable "distance" as a proxy for similarity
  6. Update numerosity through some kind of elaborate indexing node scheme
  7. Over time, perform inductive delineation using only positive examples
  8. Apply a forgetting mechanism uniformly

Image processing

Finally, at the lowest level, Phaeaco uses a library of explicit detectors for image processing. These "retinal" level structures are fundamental to the operation of the solver, and work together with the higher, "cognitive" levels of Phaeaco.

Phaeaco features a pipelined image processing model, where the processing is done gradually little by little. This apparently works nicely with the evolutionary aspects of the feature generation process. A pre-processor step does canny edge and background detection, and even desaturation, making Phaeaco somewhat future-proof in that it can operate on photo input as well.

The retinal process are (in order of presentation):

A. pixel sampler for randomisation
B. "altitude", distance from closest border
C. endoskeleton detector
D. line segment detector
E. line segment intersections
F. fill detector, by rays from source pixel
M. line intersection string elongator (??)
G. curve detector
H. noise corrector
I. dot detector
K. K-point detector
O. closed region, area and ellipse detector
P. perception node, activity in retinal nodes
R. run codelets from the Coderack
Q. quantity process
S. shrinking: blurring details, rounding off
Z. zoom, a magnifier process
X. convex hull
Y. Monte Carlo based size estimation

Conclusion: How Phaeaco solves BPs

The Phaeaco solver approach in a nutshell:

  1. Given a Bongard problem, construct visual patterns from boxes on the left and of those on the right, and
  2. Compare the patterns, and attempt to spot the difference between them.

Phaeaco tries to summarise the six boxes using three different mechanisms:

  1. Hardwired responses: nothing/something and outlined/filled
  2. Holistic view: see if anything "jumps out" from the initial population of generated patterns
  3. Analytic view: closer examination of individual boxes, generate more elaborate structures

In the holistic view, separation is based on clear statistical bi-modality. Bongard-specific codelets are employed to evaluate potential solutions. The analytic view primarily just adds new intrigue into the system by looking at each image more closely.

In short, Phaeaco is an exemplar Hofstadterian BP solver, that solves the whole multi-modal problem, if with a quite a bit of help from the user and solver designer in the form of feature descriptors and extractors.

Deep Bongard image classifier (2018)

In 2018, Ukrainian software engineer Sergii Kharagorgiev tried his hand at solving Bongard problems using a straightforward deep neural net classifier. He describes his approach and findings in a blog post. Kharagorgiev's project is very similar to what I originally had in mind, and I think is representative of what a modern brute force approach to BP solving looks like.

In his write-up Kharagorgiev describes Bongard problems as a benchmark for pattern recognition ability. The images conform to a pattern, on left and right separately. The task — the challenge for both people and algorithms — is to understand the pattern and to figure out the rule.

Kharagorgiev got started by noting that Harry Foundalis' Phaeaco relies on extensive feature extractor and detector engineering. His hypothesis was that deep learning, discovering hierarchical features automatically from data, can be useful in solving Bongard problems.

Formulation and approach

For standard machine learning tools, Bongard problems are a challenge because the puzzle instances require one-shot learning: there are only a few examples of each target concept to learn. BPs are also multi-modal, in that the input is an image, but the output is a natural language description of a classification rule.

Kharagorgiev decided to simplify the problem and treat BPs not as a challenge to verbally describe the rule that applied to the images, but purely as a classification problem. There are 6 + 6 images, which divide into 10 training samples and 2 test images, one of each kind. Given an image box, the solver needs to decide which side it belongs to.

With such a limited dataset, the only way to train a neural net is to use transfer learning: a model is trained on many examples of a similar target problem, with the relevant parts of the model then re-used in the original domain. Conveniently deep neural nets excel at learning hierarchies and can learn to detect all kinds of geometric shapes as features. These features can then be bundled into filters to power a classifier.

Kharagorgiev reasoned that training feature extraction NNs with just images from BPs was not possible, as they were too few, and too different to generalise. Instead, he constructed a synthetic dataset from random images of geometric primitives. The primitives were simple shapes with random positions, scale, rotation, possibly filled if closed. Kharagorgiev built a generator and a 1M image training set. His blog post has some great visualisations.

For Kharagorgiev's system the formulation of the training set represents the only human influence. The primitives define the finite feature set that the solver considers potentially salient for each problem. It appears that Kharagorgiev did not explore teaching explicit labels to his system (i.e., grounding the vocabulary), but learning to label detected primitives in a composite image should not be too much of a challenge for deep learning methods.

With a neural net capable of recognising geometric primitives in hand, Kharagorgiev assembled some of the net's binary feature maps into a 1050 bit vector to serve as the classifier-solver's internal representation of a given Bongard image. These binary feature vectors could then be compared using various similarity metrics. Neural net classifiers would normally learn and approximate the similarity metric in the final layers of the net, but in the case of BPs there is no general global metric to learn — the right classifier is instance dependent.

Instead, Kharagorgiev set up a simple "decision stump" classifier where the feature vectors of the images in a BP instance are evaluated bit by bit in search of correct classification. For example, if at bit position 234 the six images on the left have a "1" and the images on the right have a "0", then this bit is a potential classifier for the images.

For validation, Kharagorgiev noted that the two test images were known to be drawn from different sets, and so he could validate potential classifier bits by checking that the classifier classifies two test images as different. In this way, leveraging prior knowledge of the setup, he was able to screen the classifier bits without tainting his test set.

In the end, Kharagorgiev tested his classifier on the 232 then known Bongard problems, solving 47, of which 41 correctly — ~20% at 87% accuracy. These numbers should naturally be viewed in terms of correctly classifying one example image from both the left and right image sets, which may or may not be an accurate proxy for solving the original Bongard problem.

Discussion

In his analysis of the project, Kharagorgiev presents an insightful view of what solving Bongard problems is all about. Quoting Bongard himself (Pattern Recognition, 1967):

“...the purpose of the learning is not so much in finding a classifying rule (for example, a hyperplane), but rather in finding a feature space in which such separation is possible.”

In other words, creating the features — the right representations — is the real problem. Finding the classifier is easy after that. In this project, Kharagorgiev was searching for the feature space by way of a pre-trained image classifier neural net. Deep learning, the hierarchical view of looking at images, proved useful in this context, but it's also clear that some features require more stages of processing than is available in a pure image pattern detection pipeline.

Finally, Kharagorgiev considered the additional challenge of generating natural language descriptions for the solutions, the hyperplanes in the feature space. Natural language is easier with hand-crafted features and pattern detectors, but harder for neural nets (without a purpose-built dataset).

Kharagorgiev presents a number of interesting approaches to explore for description generation:

The multi-modal learning approach is even more brute force than a simple component classifier. The NN would try learning the function "How to solver a Bongard Problem", which sounds challenging, to say the least. Synthesising non-trivial BPs may be as difficult as solving them, and training with trivial BPs may not yield any generalisation advantage. In any case this would be a massive undertaking and would require substantial resources. What might be much more feasible is to learn labels just for components, and then separately build some processing — yes, another net would do — on top of the detected features.

Both the visualisation and generative NN approaches are interesting because they would allow completely non-linguistic Bongard solving. The visualisation route might prove a little underwhelming, as some interpretation of the output is necessary in any case. On the other hand there could well be beautiful structural ways of representing Bongard images that would yield highly pleasing expressions of the classifying hyperplanes. After all, a picture is worth a thousand words.

Similarly generating examples is in a sense a deeper way of asserting mastery over classification and category understanding beyond language constraints. This, too, leaves some room for result interpretation, but perhaps that is a fundamental aspect of Bongard problems themselves, if not of all perception and pattern recognition.

A visual language (2018)

The state of the art in Bongard problem solving (AFAIK) is found in the work of Depeweg, Rothkopf, and Jaekel (2018). In their paper, Solving Bongard Problems with a Visual Language and Pragmatic Reasoning, the authors present a solver system in which detected image features are embedded into a formal grammar, allowing Bongard problems to be framed as search in linguistic feature space.

The authors begin by stating that in 50 years of Bongard problems, only moderate progress has been made in building powerful solvers. In their view the image processing side of things is practically solved now, with modern methods being able to reliably extract visual features from Bongard images. What remains is the translation of visual primitives into structured representations that then power the higher level problem solving.

The approach the authors take in the paper is to translate visual features into a symbolic visual vocabulary, a formal language that is powerful enough to represent complex visual concepts. Through this highly structured linguistic framework, the solver can make use of more powerful methods of inference. In the paper the authors show how they apply Bayesian inference for concept induction within the context of individual BP instances.

Finally, to direct the solution search into areas of high interest, towards human preferences, the authors employ the method of pragmatic reasoning. The argument goes that as BPs feature non-random, deliberately chosen examples, it is reasonable to to view BPs as exercises in concept communication, and that this special property should leveraged in the solving process.

Introduction

The authors claim that with modern techniques "What is where?" is a solved image processing problem. Neural net image classifiers eat simple geometric shapes for breakfast, and on the other hand standard image processing libraries have mature implementations for all kinds of feature extraction. Even if there are particular, non-standard features to detect for Bongard problems, there's plenty of processing power available today to spend on custom implementations.

In other words, the authors have little interest in the feature extraction process. But there's much more to visual cognition than that: humans can reason about the visual world. Some of the authors' perspectives:

For all of the above, some higher reasoning above image processing is needed. The authors point at the long-standing debate about the relationship between vision and cognition. Is the visual system simply a sub-symbolic mechanism (perhaps a "retinal" process in Foundalis' terms)? Is reasoning about scenes better handled by a separate symbolic system?

Hofstadterians certainly believe that there is no divide, but rather a common framework for both, but whether there really is a single neural mechanism that gets applied hierarchically, is an open question.

To illustrate the nuances of the vision-cognition boundary, the authors offer amodal completion, the effect of perceiving a square when there isn't any, as an example of a perceptual phenomenon that requires contributions from both sides. Similarly some basic visual properties, such as the cardinality of things and 90 degree angles, have both pure, logical definitions as well as clear visual manifestations.

The authors suggest that perhaps a useful way to look at visual cognition is through a linguistic lens. Historically, syntactic pattern recognition was an attempt to bring symbolic techniques to bear on vision problems. Stochastic grammars and graphical models can still be leveraged in image processing today. There has been progress in combining high-level representations and noisy low-level image features in a principled manner.

As object recognition is maturing, the authors believe we will see a move towards whole scene understanding, and visual Turing tests. The challenge is to bring together computer vision, neural natural language processing (NNLP), semantic knowledge bases and reasoning systems. The quest is for the right representations: expressive enough to capture scene variation, but also compact enough to allow for efficient reasoning.

"What is the language of vision?"

Looking at Bongard problems

The authors formulate Bongard problem solving as a search in visual concept space:

"The task for a vision system is to find two related concepts that can discriminate between the left and the right side."

In the authors' formulation, solutions are logical rules given in a natural language that refers to visual features in the examples. In other words, only visual features are fair game in Bongard problems: no knowledge of the world is necessary, or rather, problems that do require side channel information are unfair.

Fundamentally, the only task for the solver is to accurately describe concepts based on given examples. The challenge is to create a vision system that can solve all (fair) Bongard problems without using ad hoc solutions for each problem.

In a review of prior work, the authors describe RF4 as an inductive logic programming system where images are hand-coded into logical formulas. They dismiss this approach as it avoids the computer vision side of the problem. Phaeaco on the other hand does work with image inputs, but the system's expressivity is rather limited.

The authors' new method is motivated by the observation that some form of recursion is need to correctly solve some Bongard problems, and therefore a language is needed. Inspired by Bongard's original vision for a solver system, they develop a three-tiered system:

  1. A visual vocabulary: image processing functions extract basic shapes and visual properties into linguistic primitives
  2. A formal language: from the vocabulary a formal language, a context-free grammar (CFG), is developed, enabling complex visual concept expression
  3. Bayesian inference: Bayesian inference is used to find sentences in this language, to best describe Bongard problems

The authors make several observations about the problem domain:

In summary, the authors focus on what they, as human Bongard solvers, perceive to be the "standard pieces". After careful analysis, the task then is to codify that insight into a formal grammar.

A visual language for BPs

The final visual grammar
Image: The final visual grammar developed by the authors. From Depeweg et al. (2018).

To build a language, you need a syntax and semantics for it. For the Bongard solving language, the authors went for a bottom-up approach to language design.

Following Bongard's lead the authors decided to call any visual object in a Bongard image a figure. The language that the authors came up with has sentences that specify logical functions over figures in the image. These functions produce output both for simple quantitative properties as well membership in complex categories. A separate evaluation function checks whether a given visual property, as defined by a figure or figures, is true for a given image. Again, the detectors solve the language grounding problem through explicit expert labelling.

The library of primitive functions they developed contains operators such as:

The authors emphasised that they used standard implementations for feature detectors wherever possible.

With the features extracted, the authors were now able to develop a context-free grammar to describe the visual data. The definition of the Bongard solving language is somewhat technical and well-described in the paper, so we'll keep thing high-level. The CFG is nothing too exciting: terminals and non-terminals, production rules and a start symbol.

Each rule describes images either on the left, or on the right. A sentence, as generated by the CFG, is a logical function that can be evaluated on an image to check whether it holds true. A solution is a sentence for the left or right side that applies to all of the images (one sometimes being a logical negation of the other).

The authors note it is sometimes a little tricky to decide whether difference in variance is perceptually meaningful. They employ log-variance within classes as a measure of relevance. They also work around issues with undefined truth values: empty sets break functions. In using their language, the authors also observed that equality and empty sets blow up the hypothesis space. These "unintuitive", human-foreign ways of looking at BP instances are taken as undefined values, effectively being excluded from being valid hypotheses.

Probabilistic model and inference

With a powerful grammar in hand, the next step is to find the best sentences. The authors note that there are many ways to go about scoring solutions and finding the best ones. Bayesian inference, standard sampling methods, has successfully been used in human concept learning, so they decided to give that a go.

In solving Bongard problems, there are usually several potential solutions to entertain. The task is to find the relative plausibility of a given solution candidate. The authors formulate the search problem as:

    P(R|E,G) = a * P(E|R) * P(R|G)

Where,

Following the lead from previous literature, the authors explore the Rational-Rules model (Goodman et al., 2008) in their solver. The idea here is that more complex rules are formed by composition as determined by the production rules. The probability of a given composite rule is a function of the productions: the rules hold the probability mass. If one adds uncertainty into the mix, it is then possible to derive the priors over rules obtained through the CFG. With the priors in hand, the Bayesian inference process can finally do its magic.

"By including uncertainty over the production probabilities one can derive a prior over rules obtained through our context-free grammar by integrating out the production probabilities using a flat Dirichlet prior."

(i.e., "some mathematical massaging allows us to distribute probability mass in a nice proportional way to the applied productions when generating sentences in our language")

The purpose of the prior is to weight the distribution by complexity, as measured by production counts. By doing this:

  1. shorter rules are favoured compared to longer rules, and
  2. rules that contain identical sub-trees are favoured, encouraging re-use.

In other words, it is more likely for a non-terminal to appear twice than it is for two different productions to occur.

Additionally, the likelihood P(E|R) is 1, if the image set E is compatible with rules R, otherwise 0. This means that 1) rule R applies to all images on a side, but no images on the other side, 2) no undefined derivations are valid, and 3) images E are informative about rule R.

The informative property of rules is inspired by pragmatic reasoning, a communications notion. It is assumed that the images were chosen to be informative. For example, if circles should be used in the answer to a given problem, circles should feature in the problem as well. The authors point out that the way informativeness is defined and implemented can have a substantial impact in practice.

In the authors' view one of their major contributions to the solution of the general Bongard problem is the establishment of pruning rules. When evaluating sentences, image sets E are rejected if they don't contain at least once each of the terminals mentioned in the rule. Similarly some functions require two objects to be informative. "Contains"-rules do not make sense if nothing is contained anywhere. Optimisations like these cut down the search space to explore.

To complete the the Bayesian inference process, the authors make use of the standard Metropolis-Hastings algorithm for sampling the posterior. With pragmatic pruning, some rule softness to allow for mistakes, smart caching, and by treating informativeness as a hard constraint, plus a couple of other tweaks, the authors finally had their solver doing inferences.

Results

The authors chose not push for solving the full back catalogue of Bongard problems. Instead they selected a subset of Bongard problems from the original set of 100. Their selection criteria were:

  1. no highly advanced computer vision technology is needed, e.g., skip occlusion
  2. no world knowledge or sophisticated object recognition: the problems are supposedly self-contained
  3. solutions are expressible in the visual language that the authors devised.

They could have extended the language to deal with specific problems, but wanted to avoid the deployment of various ad hoc constructs for individual problems.

"The limits of my language are the limits of my mind. All I know is what I have words for." (Wittgenstein)

In the end, the authors focused on a target set of only 39 Bongard problems, noting that it is not obvious whether a solution can be found, even if one is expressible in the grammar they developed. (Though surely by brute force.)

Visual language solutions
Image: Solutions to a Bongard problem in a visual language. From Depeweg et al. (2018).

Overall, the solver finds plausible solutions though not quite in the terms Bongard laid out. In the presentations, see nearby image, the problem and found rules for LEFT/RIGHT are given along with a rule probability as inferred.

Whether a rule in a formal language captures the intended natural language description is a subjective judgement, but in the authors' view the found solutions are reasonable if not always ideal. Sometimes the solver chose a more specific solution over a more abstract one. In some cases the problem itself is unclear on the presuppositions that apply: sometimes a triangle is just a triangle, but sometimes the fact that there is exactly one figure is more important. Encoding correct behaviour in these cases is a challenge. A parsimonious heuristic could prove a reasonable and useful tiebreaker for presuppositions.

Ultimately, the solver was able to solve 35 of the 39 problems in the target set, in that all the authors agreed that the discovered solution was reasonable. For 4 of the problems, the system found the intended solutions, but also shorter solutions that received higher probability. The authors believed this to be due to processing artefacts, limitations of the image processing approach.

The authors lament that there is a fundamental difficulty with regards to the evaluation of cognitive vision systems beyond object recognition. Human judges are necessary for reasonableness estimation. Quantitative evaluation is challenging due to inexact comparisons. In other words, Bongard problems are difficult to use as benchmarks. The system still handily beats Phaeaco and RF4, and so the authors claim to have made progress with the general problem.

Discussion

Bongard problems, constructed to illustrate human visual cognition, are more flexible and language-like than early pattern recognition tasks. BPs are still a challenge for modern solvers: surprisingly little progress has been made.

The authors' system uses images as input, but can still solve many of the instances. Bayesian inference and Rational-Rules priors proved a fruitful starting point. Framing the challenge as a concept communication problem led them to prune the search space through pragmatic reasoning.

Where does vision end and cognition begin? Symbolic representations throw away information about the input images. On the other hand, for basic vocabulary, the authors argue that it's easy to make the case that a human "comes equipped" with the concepts. Therefore, a focus on how primitives are combined is warranted.

It should be possible to replace the visual end (the "retinal" layer) with a more robust visual system, e.g., a neural net. On the other hand, learning might also happen at the symbolic level.

In any language there is redundancy: short expressions that help with sentence construction, or in this case, help the system find solutions. The natural motivation for this is that frequently occurring chunks become primitives themselves, with previously learned concepts getting reused. We learn to use shorthands.

The authors produced a useful language for representing simple, geometric, visual scenes. The system is not domain-general for general purpose vision. Taking triangles and circles as basic concepts is different from taking lines and corners as basic, a more detail-oriented language could prove more capable.

The aim for Bongard solvers should be to solve more and more with less and less. For the authors, this is a matter choosing the right vocabulary, the right visual language in which to express visual concepts. They are interested in using these techniques in other visual cognitive tasks as part of a quest for appropriate representations for a domain-general probabilistic language of thought.

Framing the task as a concept communication problem gave the authors a useful point of view. Solving Bongard problems, they believe, is fundamentally pragmatic problem solving. Pruning is essential for a practical system: pragmatic reasoning is a feature of high-performance systems. More problem domain definition is needed to tackle presuppositions and to account for specific examples.

The authors believe that their contribution paves the way for an architecture for visual cognition that goes beyond "What is where?".

Future work

Personally, I find that there are aspects that I like about each of the solvers I've looked at in this post. All the solvers approach the problem from a slightly different angle and with different tools. I'm intrigued by the possibility of learning from each of them, and pooling the best ideas from all of them into something new.

It's clear that the choice of feature primitives has a huge influence on the operation of any Bongard solver. Is it possible to extract features without a priori human labelling? In other words, is it possible to run a meaningful Bongard solver without grounding the inputs in language, with only a final translation step at the end? In this way, without a finite feature set, could it be possible that, for example, a neural net could pick up subtle properties about pictures and then encode them efficiently in the layers without human involvement. Side-stepping the whole language grounding problem with a fixed set of features of interest doesn't quite sound right.

As the harder puzzles rely on ever more complex and subtle structural rules, it may well be that satisfactory feature primitive detection is beyond "a pure retinal approach". In any case it would be interesting to see what exactly is possible, where and how the approach fails. If finding the right representations is the name of the game, why lock them down beforehand? Carefully crafted detectors generally don't hold a candle to those learned from data. Of course, BPs are challenging due to the indirect learning that is probably needed.

Neural nets seem to be ideally suited for capturing the fuzziness of exemplar classification. A properly trained hierarchical neural net should have not problem with considering "kind of a circle" as a true circle when necessary, and vice versa. Neural weights are infinitely versatile. The statistical route of Phaeaco feels rather flimsy in comparison.

Instead of encoding human insight into elaborate feature detectors, I wonder if it would be possible to teach primitives through examples? This is very much in the spirit of Maksimov's work as well as the mentoring in Phaeaco.

For example, if I give a neural net labelled pairs such as ([image with a circle on the right side], 85) and (cube far left, 15), could a learner pick up on the notion of "x-position"? If so, these could then be stacked and combined into a complete learner, taught one concept at a time, with smallish sample datasets. In a complex domain, perhaps machine learning is more about smart teaching? What is the best way to extend a neural net with new categories, new powers?

In other words, can we do mentoring in reverse? "What is this kind of a pattern called?" the solver asks. "That's a triangle," the solver designer replies. What's the best way to teach concept labels after they have been learned? Can we teach concepts with (a|b) examples?

I would expand on Kharagorgiev's deep learning approach by using a pre-trained network taught to find low-level features from large photograph datasets. It is almost certainly the case that humans use the same machinery for both real world visual data as well as the geometric shapes of the Bongard problems. It should be possible to take an existing network, say, an ImageNet trained ResNet, freeze the early layers, and teach the system to recognise well visual concepts of the Bongard problem type.

Another way to improve the fidelity of deep net visual recognition is to make use of data augmentation methods. This could help the detectors be invariant to figure rotation, scaling, etc. Generating synthetic, non-trivial Bongard problems is probably human-hard or at least Bongard-hard, but it's possible that there's something to be done there as well.

Exploring Kharagorgiev's suggestions for learning a variety of ways for producing natural language or analogous output from (pooled) Bongard image feature vectors is definitely worth exploring. I would also add the use of a second output net on that list. It should be fairly straightforward to learn labels for figure composites, much like sentences are generated from primitives in the work of Depeweg et al.

Foundalis makes an excellent point in his thesis, noting that solving harder problems render easier versions solved as well. The focus should absolutely be on the hardest BP instances, but with an eye towards general methods, nothing ad hoc as many of the authors agree.

If it turns out that Bongard problems are by and large too hard to solve with general means — problem specific ad hoc methods are needed — then it might be interesting to build a functional plugin system where one could select the set of detectors to use for solving Bongard problems. This would allow for Bongard solver crowd-sourcing, where people could submit plugins to solve particular instances. This could then result in a natural benchmark, where the challenge is to solve some standard Bongard problem set with the smallest possible set of operators.

I believe in the Hofstadterian vision that analogy is the core of cognition. Pattern-matching is categorisation. Every property is a dimension, a spectrum, and all things have a value somewhere along the dimension. The task is to discover categories and what properties defined them. I believe meaning resides not in objects themselves, but in the relations between them. Any measure of similarity must build on a relational notion, and it cannot be that this is something we tune by hand, it must be learned from data.

Finally, I agree with Depeweg et al. on their reasonability argument. The salience problem is made vastly easier if one views Bongard problems as concept communication tasks, and the examples as rationally selected for informativeness. The authors' approach in encoding this in their language is worth imitating. The language formulation showed its power in the inference stage, but, again, I believe there's more to the visual end than just pre-determined detector based image processing.

There is definitely room for entirely new approaches to solving Bongard problems as well.

References

Bongard, M. (1970). Pattern recognition. Hayden Book Co., Spartan Books. (Original publication: Проблема Узнавания. 1967. Nauka Press.)

Chalmers, D. J., French, R. M., & Hofstadter, D. R. (1992). High-level perception, representation, and analogy: A critique of artificial intelligence methodology. Journal of Experimental & Theoretical Artificial Intelligence, 4(3), 185–211. DOI

Depeweg, S., Rothkopf, C. A., & Jäkel, F. (2018). Solving Bongard Problems with a Visual Language and Pragmatic Reasoning. ArXiv:1804.04452 [Cs, Stat]. Arxiv

Foundalis, H. E. (2006). Phaeaco: A Cognitive Architecture Inspired by Bongard’s problems. Indiana University. Website PDF

Goodman, N. D., Tenenbaum, J. B., Feldman, J., & Griffiths, T. L. (2008). A rational analysis of rule-based concept learning. Cognitive Science, 32(1), 108–154. DOI

Hofstadter, D. R. (1979). Gödel, Escher, Bach: An eternal golden braid. Basic Books.

Hofstadter, D. R., & Fluid Analogies Research Group. (1995). Fluid Concepts and Creative Analogies: Computer models of the fundamental mechanisms of thought. Basic Books.

Kharagorgiev, S. (2018). Solving Bongard problems with deep learning. Sergii Kharagorgiev. Website

Linhares, A. (2000). A glimpse at the metaphysics of Bongard problems. Artificial Intelligence, 121(1), 251–270. DOI

Maksimov, V. V. (1975). Система, обучающаяся классификации геометрических изображений (A system capable of learning to classify geometric images), in Моделирование Обучения и Поведения (Modeling of Learning and Behavior), M.S. Smirnov, V.V. Maksimov (eds.). Nauka.

Saito, K., & Nakano, R. (1996). A concept learning algorithm with adaptive search. In Machine Intelligence 14: Applied machine intelligence (pp. 347–363). Oxford University Press.